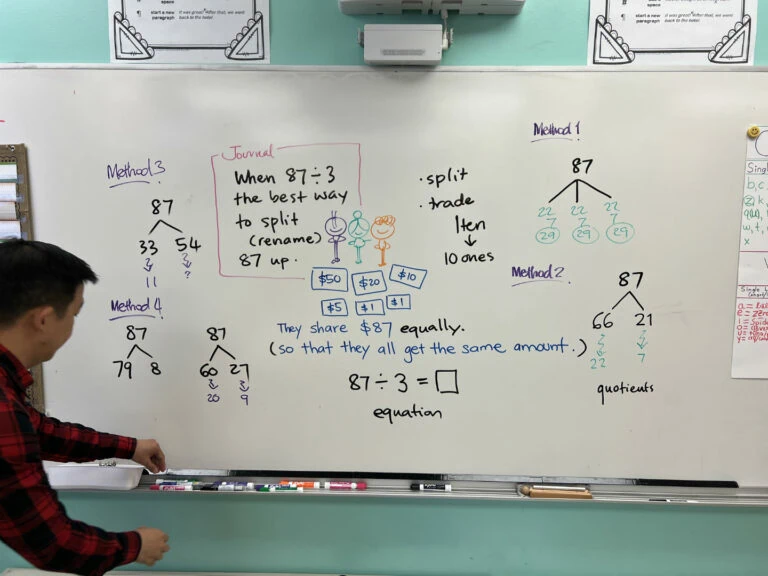
How to Rewire Your Brain to Teach Math Differently than You Learned It
By: Amy Buchheit, K-8 Math Instructional Coach at The Frances Xavier Warde School in Chicago Growing up, I considered myself “good” at math. I was good at following the rules and procedures my teachers prescribed.